
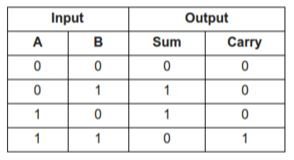
#4 bit half adder truth table full
Then the Boolean expression for a full adder is as follows.ĬARRY-OUT = A AND B OR Cin(A XOR B) = A.B + Cin(A ⊕ B) An n-bit Binary Adder Binary Addition of Two Bits 0Īs the full adder circuit above is basically two half adders connected together, the truth table for the full adder includes an additional column to take into account the Carry-in, C IN input as well as the summed output, S and the Carry-out, C OUT bit. So when adding binary numbers, a carry out is generated when the “SUM” equals or is greater than two (1+1) and this becomes a “CARRY” bit for any subsequent addition being passed over to the next column for addition and so on. Binary Additionīinary Addition follows these same basic rules as for the denary addition above except in binary there are only two digits with the largest digit being “1”. The adding of binary numbers is exactly the same idea as that for adding together decimal numbers but this time a carry is only generated when the result in any column is greater or equal to “2”, the base number of binary. This carry is then added to the result of the addition of the next column to the left and so on, simple school math’s addition, add the numbers and carry. When each column is added together a carry is generated if the result is greater or equal to 10, the base number. Type Four_Bits is array ( 1.From our maths lessons at school, we learnt that each number column is added together starting from the right hand side and that each digit has a weighted value depending upon its position within the columns. Screenshot from Atari 8-bit computer 0100 + 0000 = 0100 Carry=0 PROC FourBitAdder(FourBit POINTER a,b,s Bit POINTER c)īit InitFourBit(BYTE a FourBit POINTER res) RETURN ((Not(a) AND b) OR (a AND Not(b)))īit FUNC HalfAdder(Bit a,b Bit POINTER c)īit FUNC FullAdder(Bit a,b,c0 Bit POINTER c) V (ta, tlast) = fa4(int2bus(a), int2bus(b))Īssert(a + b = bus2int(tot), ‘totals don't match: #. To test the implementation, show the sum of two four-bit numbers (in binary). basic "gate" operations can be performed as usual bitwise operations, or they can be "wrapped" in a block in order to expose the same syntax of higher-order blocks, at implementers' choice. It is not mandatory to replicate the syntax of higher-order blocks in the atomic "gate" blocks, i.e. Solutions should try to be as descriptive as possible, making it as easy as possible to identify "connections" between higher-order "blocks". Instead of optimizing and reducing the number of gates used for the final 4-bit adder, build it in the most straightforward way, connecting the other "constructive blocks", in turn made of "simpler" and "smaller" ones. a byte) we are not interested in, you can use an extra nand ( and then not) with the constant 1 on one input. If there is not a bit type in your language, to be sure that the not does not "invert" all the other bits of the basic type (e.g. Not, or and and, the only allowed "gates" for the task, can be "imitated" by using the bitwise operators of your language. The xor gate can be made using two nots, two ands and one or. This design can be realized using four 1-bit full adders.Įach of these 1-bit full adders can be built with two half adders and an or gate. įinally a half adder can be made using an xor gate and an and gate.
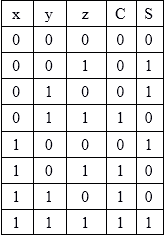
You are encouraged to solve this task according to the task description, using any language you may know.


 0 kommentar(er)
0 kommentar(er)
